최소자승법은 간단하게 말해서
"어떤 n차원 평면(공간)이 있고 이 평면 위(안)에 있지 않은 어떤 점 A가 있을때, A와 가장 가까운 평면(공간) 위(안)의 점을 찾는 것"이다.
간단해보였는데, 말해보니 간단하게 전달되지 않아보인다.
정리해보자.
1. 최소자승법 : Least Squares
어떤 행렬 $A$가 있다.
이때 이 행렬은 full column rank이다. 즉, 아래와 같은 모양을 가진다.
$$ A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \\ a_{51} & a_{52} & a_{53} \\ \end{bmatrix} $$
이때, 행렬 $A$의 열공간은 전체 5차원 공간 안에서 3차원을 span한 공간이다.

위의 그림과 같이 $A$의 열공간 $C(A)$이 평면으로 표현된다고 하자. 이 공간 안에 $A\textbf{x}$가 있고, 이 공간 밖에 벡터 $b$가 존재한다고 하자.
이때, 벡터 $b$가 열공간 밖에 있으므로, $A\textbf{x}=b$를 만족하는 해는 없다.
그렇다면 "해가 없다."하고 끝낼 것인가?
"해가 없다면, 가장 가까운 값으로 근사해보자."라는 접근으로 만들어진 개념이 최소자승법 ( Least Squares )이다.
그럼 그림을 다시 보자.
위의 그림에서 그렇다면 가장 가까운 값이 무엇이 될까?
$C(A)$안에서 표현할 수 있는 $A\textbf{x}$는 여러가지지만 그 중에 두 개만 그려보았다.
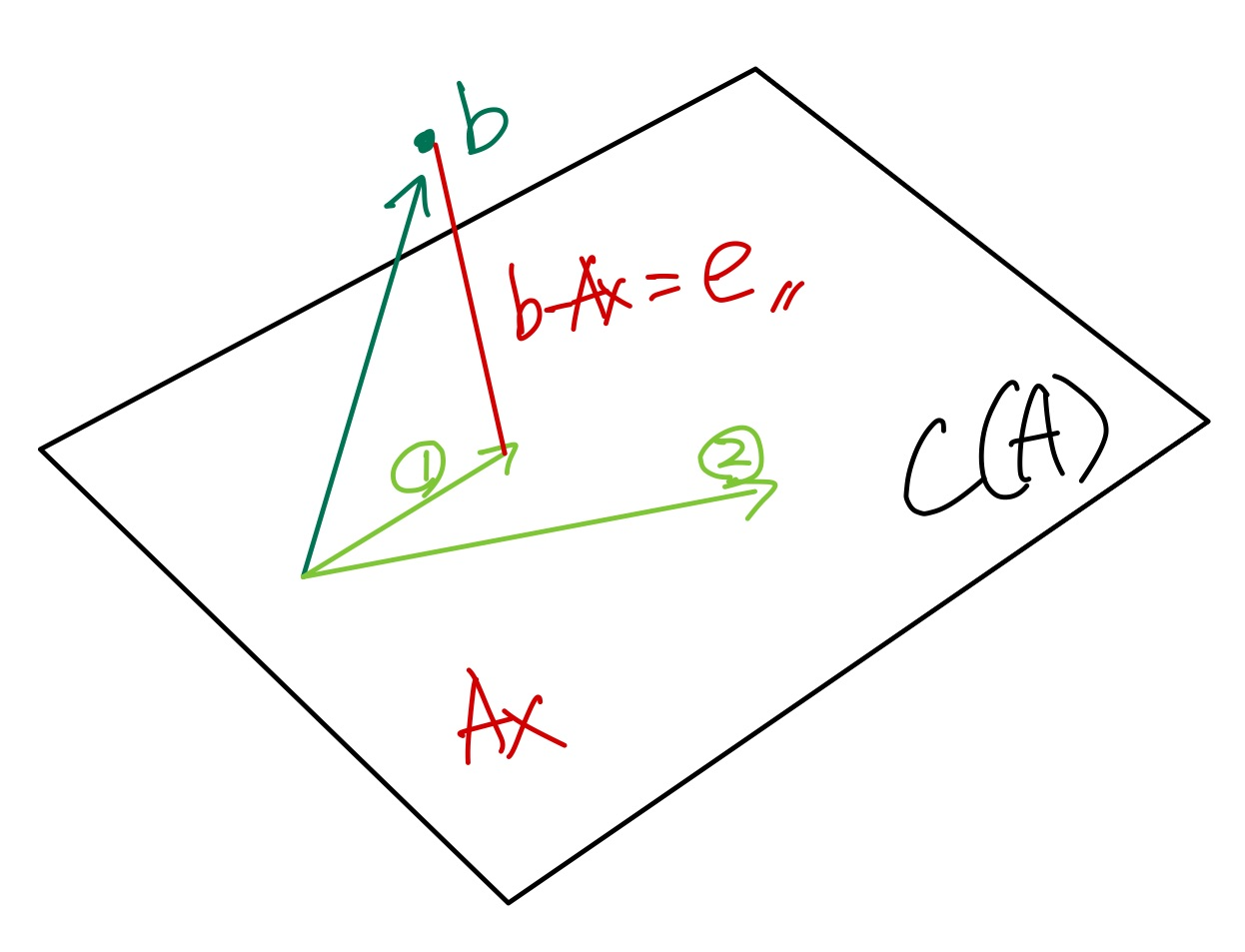
위의 그림에서 1과 2 벡터 등이 그려질 수 있다. 그중에서 직관적으로 가장 가까워 보이는 것은 1일 것이다.
우리는 이미 이러한 그림을 앞선 정사영 정리에서 보았다. 그리고 가장 가까운 벡터가 되기 위한 조건으로 벡터가 직교해야한다는 점도 안다.
그렇다면 1과 2 벡터 중에서 벡터 $b$와 직교한다면, $b-A\textbf{x}=e$ 길이가 가장 짧은 즉, 거리가 가장 가까운 벡터가 될 것이다.
최소자승법은 이러한 벡터 "$e$를 최소화하자는 접근"이다. 정확히는 "$\left\|e \right\|_{2}$($e$의 2 norm)의 제곱을 최소화"하자는 것이다. (이때, $\left\|e \right\|_{2}^{2}$은 $e$의 모든 성분의 제곱합이므로 squares가 되는것이다.)
벡터 1과 벡터 $b$가 직교한다고 하자.
그때의 $\textbf{x}$를 $\hat{\textbf{x}}$라고 할때, $b-A\hat{\textbf{x}}=e$가 최소가 되어야 한다.
두 벡터가 직교한다면, 내적이 0이므로, 다음과 같이 정리할 수 있다.
$$ (b-A\hat{\textbf{x}})^{T}A\hat{\textbf{x}}=0 $$
이를 전개해보자.
$$ (b-A\hat{\textbf{x}})^{T}A\hat{\textbf{x}}=0\\ \Rightarrow (b^{T}A-\hat{\textbf{x}}^{T}A^{T}A)\hat{\textbf{x}}=0\\ \Rightarrow b^{T}A=\hat{\textbf{x}}A^{T}A\\ \Rightarrow A^{T}b=A^{T}A\hat{\textbf{x}} \cdots (r)\\ \Rightarrow (A^{T}A)^{-1}A^{T}b=\hat{\textbf{x}} \cdots (R) $$
전개해보면 위와 같은 결과를 얻을 수 있다.
위의 $r$은 Normal Equation으로 $A^{T}A$가 정사각행렬이기 때문에 역행렬이 존재한다. 따라서, $R$과 같은 결과가 도출된다.
$R$은 $\hat{\textbf{x}}$을 구한 것이다.
이 $R$을 정사영된 벡터 $A\hat{\textbf{x}}$에 대입하면 아래와 같이 된다.
$$ A\hat{\textbf{x}} = A(A^{T}A)^{-1}A^{T}b $$
즉, 벡터 $b$에 $A(A^{T}A)^{-1}A^{T}$을 곱함으로써, 정사영된 벡터 $A\hat{\textbf{x}}$이 되기 때문에, $A(A^{T}A)^{-1}A^{T}$을 Projection Matrix라고 부르고, $\textbf{P(A)}$($A$의 열공간에 정사영하는 것이므로)라고 표현한다.
2. 최소자승법의 활용 예시
우리는 언제나 $\textbf{x}$를 알고싶다.
하지만 현실에서는 직접적으로 $\textbf{x}$을 알수 없다. 왜냐하면 일반적으로 $z=A\textbf{x}+random\;noise$ 형태로 전달이 되기 때문이다. 즉, 우리는 $z$(측정값 : measurement)를 통해 근사하는 방식으로 $\textbf{x}$를 알아내야 하는데, 이때 사용되는 개념이 Least Squares인 것이다.
단, 이때 행렬 $A$가 full column rank라는 가정이 필요하다. projection matrix나 normal equation에서 역행렬 개념을 사용해서 연산하기 때문이다. 만약 $A$가 rank-deficient라면, 역행렬을 구할 수 없기 때문에 Pseudo Inverse를 사용한다.
Pseudo Inverse 또한 중요한 개념 중에 하나로 추후 정리하도록 한다.
또, 이처럼 내적으로 풀이하는 것 말고도, 최적화 분야에서 미분으로 풀어내는 방식도 있다.
이러한 방식은 기회가 되면 정리하도록 하겠다.
'DS | Data Science > Statistics & Math' 카테고리의 다른 글
| [Linear Algebra] Part18. $rank(A)=rank(A^{T}A)$의 증명 (0) | 2024.01.13 |
|---|---|
| [Linear Algebra] Part17. 고윳값(Eigen Value)과 고유벡터(Eigen Vector) (2) | 2024.01.10 |
| [Linear Algebra] Part16. 대각합 (Trace) (2) | 2024.01.09 |
| [Linear Algebra] Part15. 행렬식 (Determinant) (2) | 2024.01.09 |
| [Linear Algebra] Part14. 역행렬 (Inverse Matrix) (1) | 2024.01.08 |